¿El pasado contra el futuro?

“Rentabilidades pasadas no garantizan rentabilidades futuras” es la muletilla que consta, en letra pequeña, en el Fondo de Inversión en el que hemos puesto la pasta para poder tener un mínimo de beneficio por ella o el recordatorio final que nos hace el gestor bancario que, después de sudar la gota gorda, nos ha medio convencido de que ese producto financiero es el que más nos conviene, no sea que nos creamos a pie juntillas el argumentario comercial que, siguiendo instrucciones, nos ha endilgado para convencernos y si la rentabilidad que obtenemos está lejos de la que nos ha comentado, nos pueda indicar que esas reclamaciones las atiende el maestro armero.

Pero, si bien esa muletilla tiene un lógico trasfondo de sentido común, lo cierto es que, además, tiene un componente teórico matemático, y para recordarlo, hemos de recordar también el número Fi (o Phi) - φ (no confundir con Pi – π, con el que nada tiene que ver), también conocido como número áureo, número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción (¡ahí es nada!)

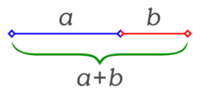
Refresquemos la memoria: hay constancia escrita de que Euclides, unos 300 años a.C. ya lo estudiaba, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica, tal como se detalla: φ es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (a más largo que b), de forma que la longitud total, suma de los dos segmentos a y b, es al segmento mayor a, lo que este segmento a es al menor b. Escrito como ecuación algebraica:

(a + b) / a = a / b = φ

Para no meternos en berenjenales y abreviar, sólo diremos que la solución positiva de la ecuación de segundo grado que se obtiene al desarrollar el cálculo es:

φ = (1 + √5) / 2 = 1,6180339887498948482045868343656381177203...

Lo curioso es que el numero Fi, siendo nada más que una cifra: 1,61803... seguido por infinitos decimales, sea uno de los números que más fascinación ha levantado a lo largo de la historia y estudiado hasta la saciedad en todas las culturas (se dice que servía de inspiración para ciertas construcciones en Babilonia y Asiria) y épocas. No son pocos los que aseguran que la Biblia está salpicada de referencias a este concepto. Por un lado, es una forma que parece gustar a Dios, puesto que tanto en las instrucciones para el Arca de la Alianza que dio a Moisés, como las que dio a Noé para la otra arca, pide unas proporciones 5x3 (casualmente, dos números de la sucesión de Fibonacci, a la que nos referiremos) que dan como resultado 1,666..., suficientemente cercano al valor de Fi como para engañar al ojo. Puestos a encontrar, hay quien encuentra relación entre 666, el número del anticristo, y el número áureo Fi.

Con esos antecedentes de fascinación no puede extrañar que en 1509 el matemático y teólogo italiano Luca Pacioli publicara un libro titulado La Divina Proporción en el que daba cinco razones por los que el número que después se conocería como Fi era eso, divino:

a) La unicidad del número, que asemeja a la de Dios;

b) El hecho de que esté definido por tres segmentos de una recta, que asemeja a la Trinidad;

c) La inconmensurabilidad del número, igual que Dios es inconmensurable;

d) Dios es omnipresente e invariable, igual que lo es este número;

e) Dios dio ser al universo a través de la quinta esencia, representada por un dodecaedro, y el número áureo dio ser al dodecaedro.

Puede que el número áureo tenga un origen divino, o puede que no. Pero desde luego su pariente aritmética, la sucesión de Fibonacci, surgió de un problema mucho más mundano, relacionado con la reproducción de los conejos, que planteó Leonardo Pisano (Fibonacci), con anterioridad a Pacioli, en su Liber abaci (Libro del ábaco) de 1202, aunque la sucesión como tal ya estaba descrita fuera de la cultura occidental en la matemática en la India, en conexión con la prosodia sánscrita, y que daba como respuesta

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, 17.711, 28.657...

en la que se observa que cada elemento de la sucesión es la suma de los dos anteriores.

Fue en 1753 cuando el matemático escocés Robert Simson hizo notar que las consecutivas divisiones entre dos elementos consecutivos (valga la redundancia) de la sucesión de Fibonacci seguían un patrón llamativo, como era ir convergiendo, alternativamente por exceso y por defecto, en el número Fi, esto es (con tres cifras decimales aquí):

1/1=1, 2/1=2, 3/2=1,5, 5/3=1,667, 8/5=1,625, 13/8=1,615, 21/13=1,619, 34/21=1,618, ....

Pero, para no perdernos, ¿de dónde viene la fascinación por Fi, la proporción áurea?

Las primeras aplicaciones de la proporción áurea son puramente aritméticas y científicas (en las que no entraremos) que desembocan en la geometría, encabezada en su representación por la espiral de Fibonacci, y estéticas, y es que investigaciones relativamente recientes acreditan que nuestros ojos analizan más eficazmente una imagen si está encuadrada en un rectángulo áureo en sus proporciones, de forma que se habría utilizado de forma intuitiva desde la Antigüedad porque es la forma más cómoda y agradable a la vista. Eso explica que en la arquitectura del Partenón, en la Gran Pirámide de Gizeh, en palacios de la antigua Babilonia… y en decenas de obras arquitectónicas a lo largo de la historia es posible encontrar ejemplos del uso de la proporción áurea (es sabido que la reconstrucción del edificio de la Universidad de Salamanca en el siglo XV estuvo guiada por ella). Pero expertos en matemáticas y arte llaman al escepticismo: tomando las medidas necesarias sería posible encontrar esta proporción en cualquier sitio, lo que no significa que fuese utilizada de forma consciente.

Entre los pintores que se dejaron seducir por las dimensiones guiadas por la proporción áurea destaca Leonardo da Vinci, pero también Salvador Dalí o los cubistas Marcel Duchamp o Juan Gris.

Dalí y un ejemplo del uso de la proporción áurea

Aunque suene paradójico, el número Fi también influye en la música, y, por ejemplo, el famoso fabricante de instrumentos Antonio Stradivarius, que vivió entre los siglos XVII y XVIII ponía mucho cuidado en situar las aberturas en sus violines en consonancia con la proporción áurea. (seguramente se tratase más de una cuestión estética que sonora, puesto que no hay indicios de que esto tenga ningún impacto en la calidad del sonido de los instrumentos) y, ceñidos exclusivamente a la música, el uso de la proporción áurea se observa en las estructuras formales de las sonatas de Wolfgang Amadeus Mozart, en la Quinta Sinfonía de Ludwig van Beethoven, en obras de Franz Schubert y Claude Debussy, aunque, claro, siempre quedará la duda de si estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras.

Llegados a este punto de comprobar la profusión de campos que están afectados por el número Fi, quizá haya que recuperar la idea de Pacioli de considerarlo divino, y es que en la naturaleza, hay muchos elementos relacionados con la proporción áurea y/o los números de la sucesión de Fibonacci. Sin ánimo de ser exhaustivos repasemos algunos ejemplos debidamente investigados:

- La disposición de los pétalos de las flores (el papel del número áureo en el campo de la botánica recibe el nombre de Ley de Ludwig)

- La distribución de las hojas en un tallo.

- La relación entre las nervaduras de las hojas de los árboles.

- La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a φ tomando como unidad la rama superior).

- La cantidad de espirales de una piña (8 y 13 espirales, números de Fibonacci).

- La distancia entre el ombligo y la planta de los pies de una persona, respecto a su altura total.

- La cantidad de pétalos en las flores. Existen flores con 3, 5 y 8 pétalos y también con 13, 21, 34, 55, 89 y 144, todos números de Fibonacci.

- La distribución de las hojas de la yuca y la disposición de las hojas de las alcachofas.

- La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol o de cefalópodos como el nautilus.

- .....

Concha del nautilus en espiral de Fibonnacci

En la vida cotidiana podemos encontrar ejemplos de esa proporción tan celebrada sin tener que irnos a un museo, contar los pétalos de una flor ni mirar a las estrellas. Las tarjetas de crédito que utilizamos a diario, las cajetillas de tabaco y hasta un simple folio son todos rectángulos áureos. Eso quiere decir que se dividimos su lado más largo por el más corto, la solución sería 1,618. Incluso donde se ha infiltrado, en este caso, la sucesión de Fibonacci, es en el juego de la Bolsa. Entre las herramientas que utilizan los analistas para intentar predecir el comportamiento de un valor (es decir, si subirá o bajará y por tanto si conviene invertir en él o no), están las proyecciones de Fibonacci. Marcan niveles en los que se pueden producir picos en la gráfica: tanto rebotes de subida si el valor está cayendo como de bajada si se encuentra al alza. El asesor financiero estadounidense Gary Meisner se ha hecho de oro creando (y vendiendo) un programa informático que diseña una cuadrícula para inspeccionar en los gráficos financieros la proporción áurea entre los índices/valores/tiempos y "guiar" al inversor en sus decisiones y, ante las quejas recibidas por su ineficacia, Meisner dice para defenderse que cuando echas la vista atrás en el mercado es bastante fácil encontrar relaciones que se ajustan a Fi. El desafío está en que mirar hacia atrás es completamente distinto a mirar por la ventana que da al frente. ¡Acabáramos! O sea, que eso de "Rentabilidades pasadas..." que veíamos al comienzo es algo más que una muletilla de prudente aviso en los Fondos y nos viene a confirmar que nada tiene que ver lo que ha ocurrido en el pasado con la construcción del futuro.

Y más allá de evidencias financieras o de elucubraciones teóricas con trasfondo pseudo-científico con excusas aritméticas, una reflexión sobre el pasado y el futuro como items vitales en todos los aspectos que se quieran considerar nos lleva a conclusiones generalizables. Un factor decisorio desde absolutamente todos los puntos de vista para diferenciar el rol del pasado con el del futuro en nosotros es admitir que el tiempo en la vida se cuenta por etapas, a veces definidas, a veces con límites confusos y a veces superpuestas, y que todas y cada una de esas etapas están identificadas (o no) por unos actores que pueden variar en cada una o permanecer en más de una, lo que no conlleva necesariamente a que el grado de protagonismo de cada actor tenga que ser directamente proporcional al tiempo o etapas en que se mantiene la relación con él.

En palabras del que fue gran poeta y pensador uruguayo Mario Benedetti,

El futuro no es
una página en blanco
es una fe
de erratas.

Y es que para analizar la relación entre pasado y futuro en el ámbito personal, hemos de partir de la base de que la vida, el futuro, es un camino que hemos de recorrer y en el que aprenderemos a través de lo que ya conocemos y también de los errores que cometemos. El inicio de este camino se llena de recuerdos en la memoria y, cuando miramos atrás, nos sentimos bien al recordarlos con nostalgia, ya que nos damos cuenta de todo lo vivido porque en la vida sólo existe el pasado y el futuro, pese a la importancia de saber aprovechar el presente siempre fugaz que avanza al mañana. Los errores se cometen, debidamente identificados y asumidos, son los que le hacen darse cuenta de cómo mejorar, de cómo ser mejor persona y, desde el punto de vista social, hace que el ser humano avance mucho más. Además, es importante señalar que, como dice el citado Benedetti, el hombre se presenta ante cada etapa de la vida con todo por hacer, y hay que estar dispuesto a vivirla de forma positiva, huyendo de posicionamientos apriorísticos, a menudo perniciosos.

Supongamos que alguien, por las razones que sean, ha de trasladarse lejos de su entorno habitual que, por duro y difícil que sea, le proporciona el confort de la familia, amigos, costumbres sociales, etc. Pero ese cambio previsto (a veces no deseado) suele comportar también que la trayectoria vital cambia radicalmente y el nuevo camino lo ha de recorrer solo, sin ningún tipo de asidero, y en el que los recuerdos, algo intangible, es lo que realmente quedará para ayudarle. Sin embargo no debe perderse de vista que los recuerdos pertenecen al pasado y, que para iniciar una nueva etapa sería un grave error anclarse en la nostalgia de un tiempo que no puede volver hasta el punto de cerrar los ojos ante la oferta de posibilidades de mejora, seguramente diferentes a las que reconocía en la etapa de la que ha salido, pero no por eso criticables ni desechables como postura ante ellas.
Volviendo a Benedetti, decía que el propio ser humano es el responsable de su destino, de su camino vital, de su trayectoria y de todo lo que en ella pase sabiendo tratar en la forma que corresponde al pasado (fuente de recuerdos que han marcado el cómo somos, que nos sirven para identificar puntos de mejora, pero nunca condicionantes del futuro), al presente (factoría constante de análisis de hechos y actitudes del pasado y su aplicación a los planes de futuro) y al futuro (siempre definido como mejora que debe encararse con la mente abierta). En resumen la "mochila", tanto emocional como de hechos, con la que cada uno llegue al final de su vida será su exclusiva responsabilidad.

Otra cosa muy diferente es la relación entre pasado y futuro colectivos. Nuevamente echamos mano de Benedetti.

Algunas claves
del futuro
no están en el presente
ni en el pasado;
están
extrañamente
en el futuro

y, cuando se habla de futuro colectivo (particularmente si su diseño se aparta del standard "oficial"), sin que se pueda aplicar a su cumplimiento la sujeción a las leyes de la probabilidad de Pascal, lo que resulta evidente es que apelar al pasado y a la historia para desactivarlo resulta de una ridiculez patética, sobre todo porque pone de manifiesto que no existen otros argumentos racionales, olvidando lo que nos dice el poema, que algunas claves del futuro sólo están en el futuro.

Como punto de partida, no parece discutible establecer que un pasado colectivo presentado como una sucesión en el tiempo de victorias bélicas queda descartado como referencia para la construcción de un futuro, salvo que éste esté diseñado, precisamente, perpetuando enfrentamientos y conflictos de vencedores-vencidos.

No es la primera vez que se reflexiona en este blog acerca del hecho de que eso que las clases gobernantes llaman historia no es sino un poderoso instrumento de manipulación política para arengar a la ciudadanía en el sentido deseado, en tanto es la narración de unos hechos escogidos de tal forma que se justifique el status político actual. Y la narración no se coarta en presentar únicamente victorias bélicas demostrativas de que "nadie nos gana" y "somos los mejores", con indiferencia de los sentimientos y actitudes de las personas y de que, en la realidad, puede ser que los tatarabuelos de quienes se ufanan de la victoria fueran, precisamente, los vencidos y aniquilados. Es más: la historia, tal como se quiere transmitir no busca los porqués, sino que se limita a alentar un "patriotismo" superficial y visceral basado en el enaltecimiento "porque sí" de la colectividad. Un par de ejemplos de que se alientan las pasiones y no el razonamiento en ese uso de la "historia": se inocula el orgullo por la victoria en la batalla de Lepanto, pero (aparte del episodio de Cervantes por su participación en ella) no se sabe dónde, cuándo o contra quién tuvo lugar ni el papel concreto de los ejércitos españoles, ni mucho menos se cita la nula repercusión de esta victoria en nuestro devenir posterior; en cambio se calla cuidadosamente en los libros la derrota de Annual, que sí que influyó en el futuro inmediato por marcar el inicio del declive del reinado de Alfonso XIII y provocar la dictadura de Primo de Rivera. La forma de narrar, además, intenta salvaguardar la opinión acerca de las clases dirigentes, y así, por ejemplo en el citado Annual, el que se enviaran 10.000 hombres a sabiendas de una muerte cierta e inútil, esconde el intento de disimular la nefasta actuación del gobierno; pasa como con el relato sobre la guerra contra la invasión napoleónica, presentada como la gesta de un levantamiento popular mientras se pasa de puntillas sobre la vergonzosa actuación de la monarquía.

No, definitivamente, los sueños de futuro colectivo no van (no pueden ir) aparejados al pasado, salvo que se quiera replicar éste, lo que permite introducir un pequeño matiz en la afirmación con la que iniciábamos estas reflexiones: “Rentabilidades futuras no justifican rentabilidades pasadas”, resaltando, para finalizar, a Benedetti: "Algunas claves del futuro están en el futuro"

De cumpleaños hoy y otros homenajes.

Hoy, 22 de octubre de 2017, además de ser el 44 aniversario de la muerte del músico catalán universal Pau Casals, nacido en El Vendrell (Tarragona), intérprete de fama mundial reconocido por su activismo en la defensa de la paz (fue nominado al Premio Nobel de la Paz), la democracia, la libertad y los derechos humanos, antifranquista convencido y declarado partidario de la independencia de Catalunya (es famoso su discurso reivindicativo, durante un homenaje que recibió en la ONU, ante Kennedy y U-Thant en el que tocó El cant dels ocells, composición tradicional catalana erigida hoy en todo el mundo en un canto a la paz), también cumple 80 años el gran poeta y también músico José Larralde. 

Centrémonos en este último. Prácticamente desconocido en España, José Teodoro Larralde Saad de nombre completo, José Larralde, Don José, "El Pampa", como se le suele llamar en su país, barbado y de voz grave, está considerado como el mejor folklorista argentino vivo y uno de los referentes más destacados de su género y de la música popular argentina, descollando, sobre todo, en la milonga campera.

Para quien no lo conozca, José Larralde¹ nació en una pequeña ciudad del interior de la provincia de Buenos Aires, en la zona donde se inicia la llanura pampeana, hijo del emigrante vasco/navarro, José Larralde Iribarren Machicote Berrotagaraicoechea, con ascendencia árabe por parte de madre, y nieto de un abuelo, que no llegó a conocer, Teodoro Larralde, que, casualidades de la vida, era luthier, fabricaba instrumentos musicales, al parecer con bastante fama en el país y en el extranjero, en el pueblo navarro de Arantza (Aranaz).

Antes de poder dedicarse a la composición y al canto, Larralde realizó trabajos de albañil, mecánico, trabajador rural, tractorista y soldador y, finalmente, como él mismo lo define, de guitarrero y cantor, aunque prosiguió trabajando en esas tareas ajenas a la música mientras realizó sus primeras grabaciones. Musicalmente tuvo un inicio de carrera fulgurante, apadrinado por otro mito, Jorge Cafrune, que lo había oído cantar en una fiesta privada en casa de un conocido común.

Larralde se ha encontrado siempre a gusto cantando para un público cercano y ha huido por sistema de promociones y concentraciones masivas, pese a lo cual su música se ha vendido en Alemania, Australia, Brasil, Chile, Colombia, España, México, Paraguay, Uruguay y Venezuela, entre otros.

Dice sus verdades con su música popular de raíz folklórica, cantando contra todo tipo de lo que él considera injusticias y desigualdades. Ciertamente, en distintas etapas, sus versos adolecieron de un cierto hermetismo y rebuscamiento. Pero si se analiza su producción en forma global, es fácil entender la adhesión de un publico que con ella valora el desprecio de Don José por la maquinaria comercial, causante, las más de las veces, de la desvirtuación del género musical que cultiva. Reacio a la hora de figurar en los medios de comunicación y de recibir distinciones, rechazó sistemáticamente a lo largo de su carrera todo tipo de premios, negándose, como curiosidad, a que se incluyera su nombre relacionado con su obra en el Diccionario de la Real Academia Española. Curiosamente, se ha de reconocer que, en términos coloquiales, construyó su carrera como le dio la gana. Pero sin embargo no será arriesgado decir que es uno de los músicos más coherentes y fieles a su labor artística que hasta ahora se han podido escuchar en la Argentina. Larralde le ha cantado al amor, a la amistad, a la soledad, a la tierra y al silencio, pero el tono social siempre estuvo representado en sus historias cotidianas.“Yo canto sobre las cosas que viví“, cuenta a la hora de explicar el porqué de su universo temático y, a la hora de expresarlo, "Más vale no diga nada si por no subir el tono me va a amordazar el alma", cantó una vez. Pero, en toda su carrera, dijo mucho sin levantar el volumen de su voz. Siempre reflexivo, tantas veces profundo.

El que suscribe descubrió la música y los poemas de Larralde hace más de cuarenta años. Hay que recordar que por aquel tiempo hubo un desembarco masivo de músicos hispanoamericanos en España, unos huyendo físicamente de la inestabilidad en sus países y otros enviando aquí su obra aprovechando el boom; así conocimos y nos familiarizamos con Atahualpa Yupanqui, Facundo Cabral, Alberto Cortez (entonces Mr. Sucu-sucu), Jorge Cafrune, Gauchos-4 (Los Arribeños en Argentina, antes de venir a España), Víctor Jara, Quilapayun y un largo etcétera, que solían tocar en directo sus obras en pequeños y oscuros antros llenos de humo que hoy no estarían autorizados, rodeados de jóvenes y no tan jóvenes ávidos de escuchar en especial las letras de sus canciones, sobre todo las relativas, y había muchas, a la denuncia social (personalmente, siempre me quedará la duda por saber si el cantor/guitarrero que acababa usualmente su actuación en el entonces conocidísimo Pub Km, de Barcelona, con una de las canciones cumbre de la resistencia chilena anti-Pinochet El cautivo de Til-Til era o no su mismísimo compositor, el exiliado músico chileno Patricio Manns). Es bueno rememorar que la llegada de esos músicos era en realidad la continuació de la tendencia iniciada en los años sesenta con el desembarco, en plena dictadura, en Barcelona (donde, a pesar de la represión, el ambiente y la convivencia social eran, como ahora, envidiables, pese a las voces interesadas en sembrar cizaña de lo contrario y se percibía ajena a la tirantez y oscurantismo del Madrid centro de poder) de un grupo de escritores sudamericanos capitaneados por Garcia Márquez, Vargas Llosa, José Donoso y, de manera intermitente, Carlos Fuentes o Julio Cortázar. Es indiscutible el ansia por la superación de la indigencia político/social de la juventud española de aquella época, que, volviendo a la música, absorbía con fruición las ideas revolucionarias de aquellas canciones, casi recreando con ello aquel fragmento de las Coplas del payador perseguido, de Yupanqui: "Si uno pulsa la guitarra pa' cantar coplas de amor, de potros, de domador, de la sierra y las estrellas, dicen : <¡Qué cosa más bella! ¡Si canta que es un primor!> Pero si uno, como (Martín) Fierro, por ahí se larga opinando, el pobre se va acercando con las orejas alerta, y el rico vicha la puerta y se aleja reculando". Y es que, en palabras de nuestro Larralde, "El cantor que no opina, no es cantor". Pero eso es otra cosa, que excede esta entrada.

Larralde nunca vino a España, y su música se difundió por medio de la radio de entonces, y no de forma masiva. Había en aquellos años entre nosotros un locutor nacido en Mendoza (Argentina), Alberto Domper², que desde Radio España, de Barcelona, dirigía y presentaba, entre otros, un programa nocturno/de madrugada en el que alternaba la música con las reflexiones, seguramente para hacer más llevadero el tiempo a los oyentes insomnes. El programa, que ya cautivaba en su presentación con la voz cálida y cercana del locutor ("... baja esa luz, deja sólo el resplandor del ventanal, y, en la penumbra de tu cuarto, sueña..."), era aprovechado por Domper para dar a conocer la buena música de su tierra, y coincidió que durante varios días programó, acompañándolas de sus comentarios, todas las piezas musicales de, concretamente, el disco de Larralde Pa' que dentre. Y fue un gran descubrimiento que dio pie a profundizar en la extensa obra poética y musical de Don José, que no decepciona.

Precisamente en ese disco Pa' que dentre figura, junto a piezas cantadas, un monumento de milonga campera que, aprovechando que hoy es el cumpleaños del autor, podemos oirlo con respeto y dedicarlo también a esas mujeres a las que se refiere la milonga, esas mujeres abnegadas, a menudo maltratadas por una sociedad insensible, que lo dieron (o le quitaron) todo sin tener nada a cambio, que eran, simplemente, una herramienta más al servicio de los caprichos y los trabajos del poderoso, herramienta de la que se prescindía sin rubor y con indiferencia cuando dejaba de necesitarse, pero mujeres que han contribuido calladamente con su sacrificio anónimo a que hoy en el fondo seamos quienes somos y a quienes les debemos un sentido homenaje, particularmente emotivo si hoy coincide también con la fecha de su cumpleaños, como ocurre con el autor.

La canción tiene por título Estatua de carne y se inicia con un canto de amor apasionado a la tierra, a su Pampa, donde la vida vive, donde muere la muerte, a la que el autor se declara apegado ("Mi tierra pampa, de allá vengo, sin haberme ido nunca, sin dejarla nunca, tratando siempre de crecer por dentro") para enlazar con la dramática descripción de la mujer india que encontró y que sacudió mi vergüenza. Nos puede parecer excesiva y lejana la descripción del personaje pero, en realidad, los casos casi como el que narra, en un cerrado ambiente rural, de mujeres sometidas por el cacique de turno y sabiendo que su vida no tenía futuro, nos son, por desgracia, muy cercanos en el tiempo, sin ir más lejos en determinados pueblos durante la relativamente reciente larga posguerra tras nuestra guerra (in)civil, tan larga que aún hoy hay facetas que parecen demostrar que el tiempo no ha pasado. ¿o realmente, por ejemplo, nos suena solamente como recurso poético que nos cueste identificar cuando Larralde nos dice de ella que hasta el peso de los brazos cansa cuando siempre se los tuvo pa´ abajo recogiendo tiempo vacío de esperanza?

Larralde consigue magistralmente despertar nuestra sensibilidad con el poema al relatarnos la explotación y el desprecio que sufre la mujer en todos los ámbitos para acabar afirmando que lo único que tiene es el silencio, y porque no da leche se lo dejan. Antes de volver a una especie de serenidad emocional con, otra vez, el recurso de la descripción de su Pampa, nos hace partícipes de la pregunta fundamental: ¿En qué lugar de la vida nace la resignación? después de admitir que el personaje se cansó de esperar nada. Y, por si quedaban dudas, pone en el altar de la comprensión y el reconocimiento que merecen el sufrimiento callado de la mujer: Me sentí tan pequeño ante tanta grandeza...

Grandes, muy grandes ellas y mezquinos, muy mezquinos quienes lo hacen o consienten. No es nuevo: ya Homero construyó en su obra La Odisea (hacia el siglo VIII a.C.) el personaje de Penélope dentro del género épico, con una clara función modélica: fundamentalmente sumisión, fidelidad, dedicación, belleza, preocupación única por los intereses del amo/esposo. En las imágenes que se conservan de esta etapa histórica se plasma el modelo de mujer joven con velo, sola, afligida, sufriente, meditabunda, dando carta de naturaleza a esa sumisión/explotación que ha llegado hasta nuestros días y que, en algunos entornos, incluso, se ha convertido en ley.
Parafraseando a Larralde, si algún día... llegara mi copla hasta tu oído, no pienses que te estoy utilizando para este sincero homenaje, sea o no la fecha de tu cumpleaños.

------------------------------

1Es interesante destacar la valoración que hace el mismo José Larralde sobre su apellido vasco: “No cambié el apellido para mi carrera artística, porque es el único y mi más sentido reconocimiento que puedo hacer por mi padre: ser un Larralde y con orgullo decir, ¡yo soy hijo de vasco!”.

2Alberto Ventura Domper, para ser exactos en su nombre completo, desarrolló casi toda su carrera radiofónica en España, después de pasar por varias emisoras de Hispanoamérica, hasta su muerte por un infarto a mediados de los años 90 del pasado siglo. Su labor profesional fue distinguida en tres ocasiones con el premio Ondas.

Las Redes y sus enredos

Como alguno de vosotros ya sabe, ayer "colgué" en mi muro de Facebook el entretenimiento que repito más abajo que, todo sea dicho, tuvo una apreciable acogida entre "compartir", "me gusta" y simples accesos, lo cual siempre es de agradecer.

 

La cosa curiosa es que ANTES de empezar a recibir reacciones al contenido del muro, ya me llegaron, como si fueran originales, sin citar el origen, copias del pasatiempo. Nada que decir, no me malinterpretéis; no se trata de copyright ni de nada parecido, y en el fondo también se agradece que alguien lo viera, le gustara y decidiera reproducirlo, aunque fuera como propio, sin citar la fuente.

 

Pero, cavilando sobre este hecho, en este caso totalmente intrascendente, es inevitable pensar en lo fácil que es propagar bulos, rumores, comentarios tendenciosos o simples mentiras. Hay personas, bienintencionadas, por supuesto, que tienden a creer a pie juntillas TODO lo que aparece en las Redes, a menudo SÓLO porque aparece en ellas, sin tomarse el tiempo necesario para contrastar su veracidad. Y hay personas, éstas menos bienintencionadas, que, conocedoras de esa tendencia heredera de la buena fe, la aprovechan impúdicamente para extender y amplificar sus sesgos o falsedades interesados, de forma que, frecuentemente (como pasó con la anécdota de mi muro), la actuación espontánea de quien los reproduce sin remitirse a la fuente imposibilita llegar a ella, si es que el tema aconseja hacerlo, y todo se convierte  en un run-run, en un "me han dicho que  han oído que decían..." sujeto únicamente a la credibilidad que merezca al lector la última persona que lo reproduce. Y así nos va...

¡Ah! A mayor abundamiento, el pasatiempo tampoco es originalmente mío; es una modificación/adaptación de uno que encontré hace tiempo en las Redes, de autor desconocido.

Del cuadrado mágico al sudoku

Hace algún tiempo, concretamente cuando se cumplía su 500 aniversario, tuvimos el atrevimiento de dedicar una entrada de este blog al cuadrado mágico que aparece en el grabado de Alberto Durero Melancolía I, a su misterio, a la fascinación y a la atracción que sigue provocando a quien lo contempla con un cierto detenimiento.

Desde esa fecha hemos recibido comentarios (esporádicos, no continuados, que nadie piense en agobios, en una demostración no estadística de que las matemáticas, aún las recreativas, causan un inevitable repelús en la parroquia, que prefiere decantarse por otros temas para dedicar su tiempo, incluso los relacionados con la política [!!] por considerarlos más livianos [!!!!] y que no exigen tanta concentración) centrados en su mayoría en saber si puede haber cuadrados mágicos de mayor tamaño que el de Durero y si encajan aquí los hoy populares sudokus.

Para empezar, un cuadrado mágico es una tabla donde se dispone de una serie de números enteros en un cuadrado de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma. Usualmente los números empleados para rellenar las casillas son consecutivos, de 1 a n², siendo n el número de columnas y filas que forman el cuadrado mágico.

El cuadrado de 1 fila x 1 columna tiene, lógicamente, una sola casilla en la que, siguiendo la definición, colocamos el número 1, luego, de magia, poca.

Igualmente, en el caso de 2 x 2 es imposible construir con los cuatro números del 1al 4 un cuadrado mágico.

La cosa se anima para el cuadrado de 3 x 3, en el que los dígitos del 1 al 9 pueden disponerse de ocho formas para alcanzar la "magia".  

"Soluciones" cuadrado mágico 3 x 3

Pero no hagamos trampa: cada uno de los ocho cuadrados mágicos resultantes es realmente el mismo porque se obtiene mediante rotaciones o reflexiones de él; se conviene, pues, que sólo existe una solución auténtica para el cuadrado mágico de 3 x 3, sea cual sea su presentación gráfica.

Sorprendentemente, a partir de 3 x 3, el número de cuadrados mágicos que pueden construirse crece a un ritmo de vértigo. Para el 4 x 4, en el que se encuadra el de Durero, sin considerar rotaciones y reflexiones de la figura, es posible crear 880 cuadrados mágicos diferentes. Para un cuadrado de 5 x 5, el número de resultados posibles (calculado informáticamente en 1973) es de 275.305.224, y para el cuadrado de 6 x 6 ni siquiera se conoce el número, aunque los matemáticos creen como probable la cifra de un 1 seguido de 19 ceros.  

Grabado "Melancolía I", de Durero, donde aparece el cuadrado mágico.

Hay una curiosidad adicional que no nos resistimos a señalar con el cuadrado mágico de Durero, y es que, si se gira 180º y se resta 1 en las casillas que contienen los números 11, 12, 15 y 16 se obtiene el cuadro de Gaudí, que se puede contemplar esculpido en un lateral del Templo de la Sagrada Familia, de Barcelona. Realmente, este cuadrado no es mágico, pues tiene números repetidos, pero es bastante especial: las filas, columnas y diagonales suman 33, la edad de Cristo al morir.  

Cuadrado de Gaudí

Si hablamos de cuadrados mágicos no podemos olvidar a uno de sus estudiosos y entusiasta más notable: Benjamin Franklin, de quien se cuenta que, para matar el aburrimiento que le producían los debates en la Asamblea de Pensilvania, de la que era secretario, construyó una célebre variante de cuadrado de 8 x 8, que publicó en su obra Experiments and observations on electricity, en 1769. Formalmente no es un cuadrado mágico porque, aunque cumple con la regla de las sumas de las filas y de las columnas, siendo la constante del cuadrado 260, no cumple con la regla de la suma de las diagonales principales,sustituídas éstas por "diagonales quebradas", esto es, que partiendo de una esquina, van hacia el centro y vuelven desde él a otra esquina haciendo la forma de una V., y encierra otras simetrías seductoras, como que la suma de los números contenidos en cualquier subcuadrado de 2 x 2 es 130, igual que la suma de cuatro números cualesquiera equidistantes del centro. 

  

Cuadrado 8 x8 Bejamín Franklin

Se dice que Franklin creó varios cuadrados mágicos a lo largo de su vida, y se cuenta como cierta la proeza de que, en una sola tarde, compuso un increíble cuadrado de 16 x 16, que reivindicó como "el más mágicamente mágico de todos los cuadrados mágicos jamás creados por cualquier mago". Sin comentarios.

Cuadrado 16 x 16 Franklin

Y llegamos al sudoku. Ciertamente su base teórica se inspira, aunque sea lejanamente, en los principios matemáticos del cuadrado mágico, pero si bien éste está reservado a mentes auténticamente privilegiadas, el sudoku está pensado para que la gran mayoría de simples mortales puedan acceder ¡y disfrutar! con el pasatiempo. Porque es eso: un pasatiempo.

Contrariamente al cuadrado mágico, cuyo origen se pierde en la noche de los tiempos¹, el sudoku es un invento moderno, de nuestros días, y tiene aquello que llamamos ficha de trazabilidad con fechas, nombres y apellidos. El sudoku, con el nombre de number place, fue inventado en 1979 por el arquitecto americano Howard Garns; fue rediseñado a la forma que le conocemos ahora y bautizado como sudoku (expresión japonesa que se puede traducir por "el número debe aparecer sólo una vez" o, más llano, "solución única") por el japonés Maki Kaji en 1980 y lanzado al gran público a iniciativa del juez jubilado neozelandés Wayne Gould, a través de negociaciones a lo largo del tiempo con empresas editoras de periódicos a partir de 1997. Hay que decir que la aceptación del pasatiempo por el público fue prácticamente inmediata: en 2004 sólo insertaba sudokus en sus páginas el Times; en 2005 se le unió el Daily Telegraph; en 2006 ya publicaban sudokus diarios de sesenta países y, a finales de 2007, ya eran noventa los países, hasta llegar a nuestros días en que se pueden encontrar casi en cualquier diario que caiga en nuestras manos, estemos donde estemos.

Pensando en quien, por diferentes razones, no ha tenido oportunidad de cavilar descifrando los entresijos del juego, diremos que se basa en una tabla (cuadrado latino técnicamente) de 9 x 9 de tal forma que todas las casillas se han de rellenar con dígitos del 1 al 9 con el requisito de que no puede haber ninguna repetición de ningún dígito en ninguna fila ni columna. Hay una condición adicional: el cuadrado de 9 x 9 se divide en 9 subcuadrados de 3 x 3, señalados con un trazo más grueso, y cada número, del 1 al 9, sólo puede aparecer una vez en cada subcuadrado. Para que el juego responda al nombre de sudoku, es decir, tenga una solución única, se proporcionan entre 25 y 30 números/pista correctamente colocados. No es un capricho lo de las pistas correctas: la cadena Sky TV anunció que emitiría un programa sobre sudokus y lanzó como señuelo premiar la correcta resolución de uno de presentación. Con el fin de darle más vidilla al asunto y valorar más la respuesta correcta, de motu propio decidió alterar las pistas (no consta de qué forma, pero cabe pensar que eliminando una). La sorpresa fue que en poco tiempo empezaron a recibir respuestas correctas pero diferentes, lo que representó un fiasco absoluto y el programa no se emitió. Posteriormente se supo que la alteración en lo que devino un falso sudoku daba lugar a obtener 1.950 soluciones correctas.

Hemos apuntado que en los diarios se suelen proponer sudokus con entre 25 y 30 pistas; un ordenador potente, provisto del programa informático adecuado, puede hallar la solución del pasatiempo hasta con un mínimo de 17 pistas, y los expertos matemáticos estiman imposible la resolución de uno con sólo 16 pistas.

La pregunta que es posible que se hagan muchos aficionados es la de si, a la vista de la globalización del pasatiempo, está cercano el tiempo en que se publiquen sudokus repetidos. La respuesta ha de llevarles tranquilidad; aplicando un relativamente sencillo cálculo combinatorio a las premisas de cuadrado latino de 9 x 9 con subcuadrados de 3 x 3 incluyendo cada uno de ellos los dígitos del 1 al 9, el número de cuadrados posibles para ser sudokus es de 6 seguido de 21 ceros. Para no hacer trampas, eliminando los que sean rotaciones o reflexión de otro (como hemos detallado que ocurre en el cuadrado mágico de 3 x 3), el número que queda de posibles sudokus distintos es sólo de unos 6.000 millones. No se acaba el mundo con ellos, no.

¿Alguien se atreve a probar?

------------------------

1El cuadrado mágico de 3 x 3, cuyas filas, columnas y diagonales suman 15, ya aparece citado en la cultura china unos 1200 años antes de nuestra era con el nombre de lo shu, del que creían que simbolizaba las armonías internas del universo, y lo utilizaban para la adivinación y la adoración.

Jueces, fiscales y blanqueo de capitales.

Los pasados días 25 y 26 de septiembre tuvo lugar en Quito (Ecuador) un Taller de trabajo organizado por GAFILAT, agencia regional para Latinoamérica  del GAFI, cuya celebración ocupó entre nosotros un lugar irrelevante  en las parrillas de los noticieros, más volcados en los últimos tiempos (con mayor o menor veracidad, todo hay que decirlo) en cosas domésticas. Pero conviene no olvidar el evento, que responde al largo y revelador nombre de El papel de los jueces y fiscales en la lucha contra el blanqueo de capitales y la financiación del terrorismo: experiencias, desafíos y mejores prácticas, de la misma forma que conviene no olvidar tampoco la inmoral lucha denodada que libra el colectivo mundial de abogados/asesores para que su participación (a veces plenamente consciente) en esos delitos quede impune.

En el resumen de prensa del Presidente que se ha divulgado el 5 de octubre sobre los resultados del Taller, consta que se añadieron debates sobre las mejores prácticas en la investigación y enjuiciamiento del blanqueo de capitales y la financiación del terrorismo y la confiscación de los productos del delito, habida cuenta de la diversidad de las normativas nacionales.

Los aproximadamente 70 delegados que representaban a 21 delegaciones, incluidos conocidos fiscales expertos en la prevención del blanqueo de capitales y de la financiación del terrorismo, jueces de instrucción y jueces compartieron ejemplos de cómo superar estos desafíos y discutieron mecanismos efectivos y buenas prácticas.

Tras la experiencia con los colectivos de abogados, la divulgación a los Servicios de Fiscalías y al Sistema de Justicia Penal y su compromiso es una de las Prioridades del GAFI para 2017-2018 considerando que el poder judicial tiene un papel esencial en el establecimiento de instituciones estables, la rendición de cuentas, la integridad, la transparencia y el estado de derecho, que son todos los pilares de un sistema eficaz de la prevención del blanqueo de capitales y de la financiación del terrorismo.

No se piense que la casuística de trabajar en esta concienciación se limita a territorios complejos como los países latinoamericanos, no: el taller de Quito ha sido el primero de una serie de talleres que el GAFI y sus agencias regionales organizarán conjuntamente este año. El próximo taller tendrá lugar en enero de 2018 para los jueces y fiscales de la región de Asia y el Pacífico y se organizará conjuntamente con las agencias del Grupo Eurasiático y el Grupo de Asia y el Pacífico sobre Lavado de Activos.Los resultados de los debates de estos talleres contribuirán a un documento final del GAFI que identificará los desafíos reales que enfrentan los fiscales y el poder judicial y sugerirá buenas prácticas para tratar con ellos. Esto debería mejorar la eficacia de los servicios de la fiscalía y los sistemas de justicia penal para enjuiciar a los terroristas y criminales que abusan del sistema financiero y confiscar los bienes relacionados con la delincuencia. No deja de resultar llamativo en este punto que, si bien es cierto que ya desde 1990 (Convenio relativo al blanqueo, seguimiento, embargo y decomiso de los productos del delito, hecho en Estrasburgo el 8 de noviembre de 1990 y ratificado por España y publicado en el BOE 252/1998, de 21 de octubre de 1998) había gran preocupación por conseguir retornar los productos del delito, resulta un hecho que, por razones variadas, jurídicas y extra-jurídicas, aún vemos con auténtica estupefacción como es habitual que el delincuente entre (o no) en prisión pero no devuelve ni un céntimo de lo conseguido con su participación en el delito porque argumenta que ha sido "dentro de la legalidad", lo que, junto con la observación de otras acciones que nos dicen que están "fuera de la ley", nos debería hacer replantearnos la justicia de nuestro sistema normativo.

El GAFI, dice el resumen de prensa, continuará centrándose en mejorar el compromiso con los servicios nacionales de fiscalización y otros instrumentos expertos dentro de los sistemas de justicia penal para crear sinergias y, en última instancia, mejorar la eficacia de los esfuerzos en la prevención del blanqueo de capitales y de la financiación del terrorismo a través de la unificación de criterios.

Relaciones personales y política, ¿amistades peligrosas?

El número Pi (π) es, seguramente, el número mas estudiado (y más aclamado) de las matemáticas. Se cree que su origen se remonta al año 2000 a.C y representa una de las constantes matemáticas más importantes utilizada habitualmente en matemáticas, física e ingeniería. Se encuadra dentro de los llamados número irracionales trascendentes¹, como demostró el matemático alemán Carl Louis Ferdinand von Lindemann, por lo que no es un número exacto sino un número infinito, con infinitas cifras decimales.

El número es la constante que relaciona el perímetro de una circunferencia con la medida de su diámetro: π= L/D, siendo L la longitud o perímetro de la circunferencia y D su diámetro.

Habría que esperar al siglo XVII para convertir esa correlación en un dígito y para que acabara siendo bautizado finalmente con el nombre de "Pi" (del griego periphereia, término para designar el perímetro de un círculo). La notación fue usada por primera vez en 1706 por el matemático galés William Jones y popularizada por Euler en la obra "Introducción al cálculo infinitesimal" de 1748.

El valor numérico de π, limitado a sus primeras cifras, es el siguiente:

π ≈ 3.14159265358979323846 …

El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia: el matemático inglés William Shanks consiguió en 1853 obtener 707 decimales del número pi tras un trabajo de investigación de casi 20 años (la salvedad de este hito matemático es que cometió un error en el 528º decimal, por lo que el resto desde ese decimal estaban todos mal) hasta la actualidad, en que los ingenieros informáticos Shigeru Kondo y Alexander J. Yee han descubierto hasta 10 billones de decimales de este número irracional (un billón americano es la mitad de uno español, lo que no desvirtúa la enormidad de la cifra).

Debido a que este número sirve para calcular el área de un círculo, su perímetro o el volumen de un cilindro, se aplica a la fabricación de neumáticos, botellas, vasos o relojes. En astronomía, también se utiliza (por la NASA), por ejemplo, para calcular la cantidad de hidrógeno que se requiere en las misiones espaciales o para calcular las extensiones de territorio de los diferentes planetas. También tiene gran utilidad en estadística, en trigonometría o en topografía.

Como curiosidad, el músico Michael Blake, nos hizo ver cómo se podían convertir los sonidos de pi en una canción, pues asignó una nota musical a cada número y posteriormente tocó una melodía con un gran éxito en las redes sociales.

Se trata de un número tan aclamado que cuenta hasta con su propia celebración. El 14 de marzo (3/14, con notación americana, claro) a las 01:59 PM es el momento cumbre de la celebración, por la aproximación de seis dígitos: 3,14159.

Precisamente la particularidad apuntada más arriba de que Lindemann demostró que π es un número trascendente, tuvo impacto definitivo en un problema geométrico que venía de antiguo: resulta que, ya desde la época de Pitágoras (de antes no hay registros) los matemáticos tenían el pasatiempo recurrente de, con sólo regla y compás (es decir, con las magnitudes de los valores geométricos gráficos obtenidas sólo con esas herramientas), calcular y dibujar diferentes formas poligonales que tuviesen la misma área de superficie. Y todo iba bien hasta que decidieron intentar calcular y dibujar un cuadrado que tuviese la misma superficie que un círculo dado. Ahí se atascaron, lo que dio más popularidad al problema y llevó a que fueran muchos más, a lo largo de los tiempos, los que intentaran resolverlo, y algunos, como el pensador inglés Hobbes, afirmaran haberlo hecho (en este caso fue refutado por John Wallis "el matemático más brillante después de Newton"), hasta que Lindemann demostró en 1882 que, al ser π un número irracional trascendente, la operación es imposible (la demostración matemático/geométrica es muy compleja y queda fuera de la liviandad de estas líneas; habréis de confiar en mí de que esto es así). Desde entonces, la expresión "cuadratura del círculo", procedente de la jerga matemática, se usa para aludir a algo irrealizable o imposible... o que nos lo venden así en cualquier ámbito.

Es lo que nos pasa ahora, en estos complicados momentos que estamos viviendo, en los que algunos quieren imbuirnos (sin calibrar las consecuencias) de que armonizar los sentimientos en general, y la amistad en particular (para dejar en otro nivel las relaciones familiares), con la política es como intentar la cuadratura del círculo.

Pero ¿es así de verdad? Veámoslo de entrada en el plano teórico.

La amistad es un sentimiento desinteresado y puro que une a los seres humanos, que por intermedio de la confianza, lealtad, sinceridad o apoyo construyen una relación de afecto. La amistad es tan valiosa que hasta en las Sagradas Escrituras podemos encontrarla así: “Un amigo fiel es escudo poderoso; el que lo encuentra halla un tesoro. Un amigo fiel no se paga con nada, no hay precio para él. Un amigo fiel es bálsamo para la vida, los que temen al Señor lo encontrarán”. Las personas necesitan de la amistad que, además de necesaria, es bella. Decía Aristóteles que “los amigos se necesitan en la prosperidad y en el infortunio, puesto que el desgraciado necesita bienhechores, y el afortunado personas a quienes hacer bien. Es absurdo hacer al hombre dichoso solitario, porque nadie querría poseer todas las cosas a condición de estar sólo. Por tanto, el hombre feliz necesita amigos”

La política es (debe ser) el arte de servir, que propende, en la búsqueda del bienestar general, a lograr objetivos colectivos que conduzcan a mejorar las condiciones de vida de una sociedad para garantizar una convivencia en paz, con satisfacción plena de sus necesidades y el bienestar de toda la gente.

Analizando los dos conceptos podemos deducir que, en teoría, son concepciones semejantes que podrían coexistir y complementarse, para que de la mano construyan una sociedad más equitativa, estable y con las bases esenciales para lograr el desarrollo y progreso que la guíe al mejoramiento de las condiciones de vida de cada uno de sus integrantes.

Inventando/magnificando lo que quieren que veamos

Pero por el contrario, en muchos casos encontramos que son contraposición la una de la otra, y que en ocasiones llega a ser un detonante para que el odio y el desprecio se apoderen de la condición humana, lo que nos lleva a vivir en un mundo de penuria y resentimiento que nos impide vivir en armonía y en paz hasta con nosotros mismos. Si eso es así, sólo caben dos interpretaciones: o la amistad no es amistad o la política es otra cosa diferente a la definida más arriba.

Es de sobras conocido que la política, junto con la religión, el deporte y algún tema más, se convierte frecuentemente en un tabú en las relaciones, pero, bien mirado, si el respeto a la persona es auténtico, también lo debe ser el respeto a sus ideas, aunque estén en las antípodas de las propias. Por eso recordaremos que, en el plano teórico, hay tácticas que se pueden usar para hablar de política sin dañar relaciones, insisto, siempre que sean auténticas, a pesar de tener diferencias importantes de opinión.

1: Primordial: no fuerces a hablar de política, especialmente si desconoces a las personas en el grupo al que te diriges o si sabes que hay alguien con un punto de vista muy distinto al tuyo ya que podrías dejarte llevar por las emociones. Recuerda que la política realmente es un tema divisorio que puede tener consecuencias sociales potencialmente desastrosas en el tratamiento de su diversidad.

2: Infórmate antes de hablar. Si has decidido hablar de política, infórmate bien antes de abrir la boca. La manera más fácil de perder el respeto de otros y de, a su vez, faltarles el respeto es promoviendo la propaganda y desinformación de un partido político o ignorando los hechos e inventando cosas.

3: Mantén la mente abierta. Hablar de política, cuando se hace con respeto y entre personas informadas, puede ser estimulante y hasta divertido. Sin embargo, no hay nada más frustrante que conversar con alguien que solo da a conocer sus puntos de vista sin escuchar o menospreciando a los otros. Tómate el tiempo para verdaderamente escuchar y entender los argumentos de la otra persona. De esta forma la conversación será más agradable y seguro aprenderás algo de tu interlocutor, independientemente si compartes su manera de ver el mundo.

4: Aprende a identificar cuándo es el momento de cambiar de tema. A veces los debates políticos aumentan demasiado los niveles de intensidad. En esos casos es mejor cambiar de tema. El silencio es una manera de decir que has terminado de hablar sobre ello y que le has dado la última palabra a tu interlocutor.

5: Cuidado con las redes sociales. Las redes sociales nos permiten compartir nuestros puntos de vista instantáneamente y con una gran cantidad de personas, por lo que hay que ser precavido con los comentarios políticos. Sí, seguramente generarán mucha discusión, pero debido a que la discusión es virtual, es fácil malinterpretar comentarios y casi imposible detectar el sarcasmo.

6: Nunca lo tomes como algo personal. Las amistades y los puntos de vista diferentes son perfectamente compatibles. Hay que aprender que posturas diferentes, incluso opuestas, a la propia no deben tomarse como ataques personales o contra los ideales: son simple y llanamente otros puntos de vista.

Si se dan por buenas y aplicables estas sugerencias, estamos admitiendo que lo importante es la persona y su equilibrio y que en los casos en que la política se impone y afecta negativamente a las relaciones personales, lo que flaquea es la integridad de la persona, sea por carencias propias insalvables, sea porque políticos irresponsables (apoyados usualmente por los medios a su servicio) aprovechan precisamente esas carencias, las magnifican y manipulan sin vergüenza, y sin pensar en las consecuencias, a su favor.

Como decía una famosa canción popularizada por el grupo Los Módulos en los años 70 del pasado siglo, "Todo tiene su fin", y cuando acaba un debate, controversia o confrontación políticas, al margen de cuál sea el resultado y sus efectos políticos, seguimos teniendo los mismos vecinos, la misma familia, los mismos amigos (hay que ser sinceros en este apartado: los mismos excepto quizá, por desgracia, quienes en su debilidad se han dejado intoxicar por unos u otros y no han sido capaces de valorar a las personas sino a las etiquetas que ellos mismos le han puesto, es decir, en definitiva, quienes proclaman con sus hechos que lo suyo no era amistad sino otra cosa), seguimos yendo a las mismas tiendas, usamos los mismos servicios, acudimos a los mismos religiosos o policías, etc. Es, pues, una locura plantear cualquier diferencia política (por relevante que sea; es más, cuanto más relevante, menos debe plantearse así) como un asunto de vencedores y vencidos, empezando por la irresponsabilidad de presentar a los partidarios propios como "hombres de bien", los "buenos", alentando la idea de que "ellos" son "los malos", merecedores de todos los castigos. La estrategia del mal político que usa estos métodos se acompaña para aumentar su eficacia del bombardeo por parte de los medios afines de consignas únicamente desde el punto de vista propio silenciando o menospreciando los argumentos del contrario en un cliché repetitivo de la idea principal, de "nosotros somos los buenos y nos es igual lo que piensen ellos, que no queremos ni saberlo porque les ganaremos porque tenemos los medios de nuestra parte". Cuando un contendiente político usa estas armas perversas de confrontación entre personas está exhibiendo una grave incompetencia política al pregonar que, en realidad, no tiene argumentos aunque tenga el poder y, lo que es mucho peor, hace gala (y un sector de la ciudadanía, asombrosamente, lo jalea) de que le trae sin cuidado la imprescindible concordia del futuro.

Es triste constatarlo, pero cuando se presenta una contienda con ese marco (y se presentan, vaya si se presentan) y se pregunta al ciudadano medio del bando "vencedor" cuáles son los argumentos del contrario, se pueden contar con los dedos de una mano los que dicen algo coherente más allá de las consignas que le han imbuído.

En definitiva, las relaciones humanas y la política (o las religiones, o el deporte, o... ) no son (no deben ser) una "cuadratura del círculo", son plenamente compatibles, y cuando no lo son, lo que falla es la persona, sin olvidar la insensatez de algunos políticos en agrandar esos fallos con falaces manipulaciones que, por cierto, como se ha apuntado, no tienen como objetivo un bienestar colectivo y común de futuro.

--------------------------------------

1Un número trascendente, también número trascendental, es un número real o complejo que no es raíz de ninguna ecuación algebraica con coeficientes enteros no todos nulos.Un número real trascendente no es un número algebraico, pues no es solución de ninguna ecuación algebraica con coeficientes racionales. Tampoco es número racional, ya que estos resuelven ecuaciones algebraicas de primer grado, al ser real y no ser racional, necesariamente, es un número irracional. En este sentido, número trascendente es antónimo de número algebraico. La definición no proviene de una simple relación algebraica, sino que se define como una propiedad fundamental de las matemáticas.