Del cuadrado mágico al sudoku

Hace algún tiempo, concretamente cuando se cumplía su 500 aniversario, tuvimos el atrevimiento de dedicar una entrada de este blog al cuadrado mágico que aparece en el grabado de Alberto Durero Melancolía I, a su misterio, a la fascinación y a la atracción que sigue provocando a quien lo contempla con un cierto detenimiento.

Desde esa fecha hemos recibido comentarios (esporádicos, no continuados, que nadie piense en agobios, en una demostración no estadística de que las matemáticas, aún las recreativas, causan un inevitable repelús en la parroquia, que prefiere decantarse por otros temas para dedicar su tiempo, incluso los relacionados con la política [!!] por considerarlos más livianos [!!!!] y que no exigen tanta concentración) centrados en su mayoría en saber si puede haber cuadrados mágicos de mayor tamaño que el de Durero y si encajan aquí los hoy populares sudokus.

Para empezar, un cuadrado mágico es una tabla donde se dispone de una serie de números enteros en un cuadrado de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma. Usualmente los números empleados para rellenar las casillas son consecutivos, de 1 a n², siendo n el número de columnas y filas que forman el cuadrado mágico.

El cuadrado de 1 fila x 1 columna tiene, lógicamente, una sola casilla en la que, siguiendo la definición, colocamos el número 1, luego, de magia, poca.

Igualmente, en el caso de 2 x 2 es imposible construir con los cuatro números del 1al 4 un cuadrado mágico.

La cosa se anima para el cuadrado de 3 x 3, en el que los dígitos del 1 al 9 pueden disponerse de ocho formas para alcanzar la "magia".  

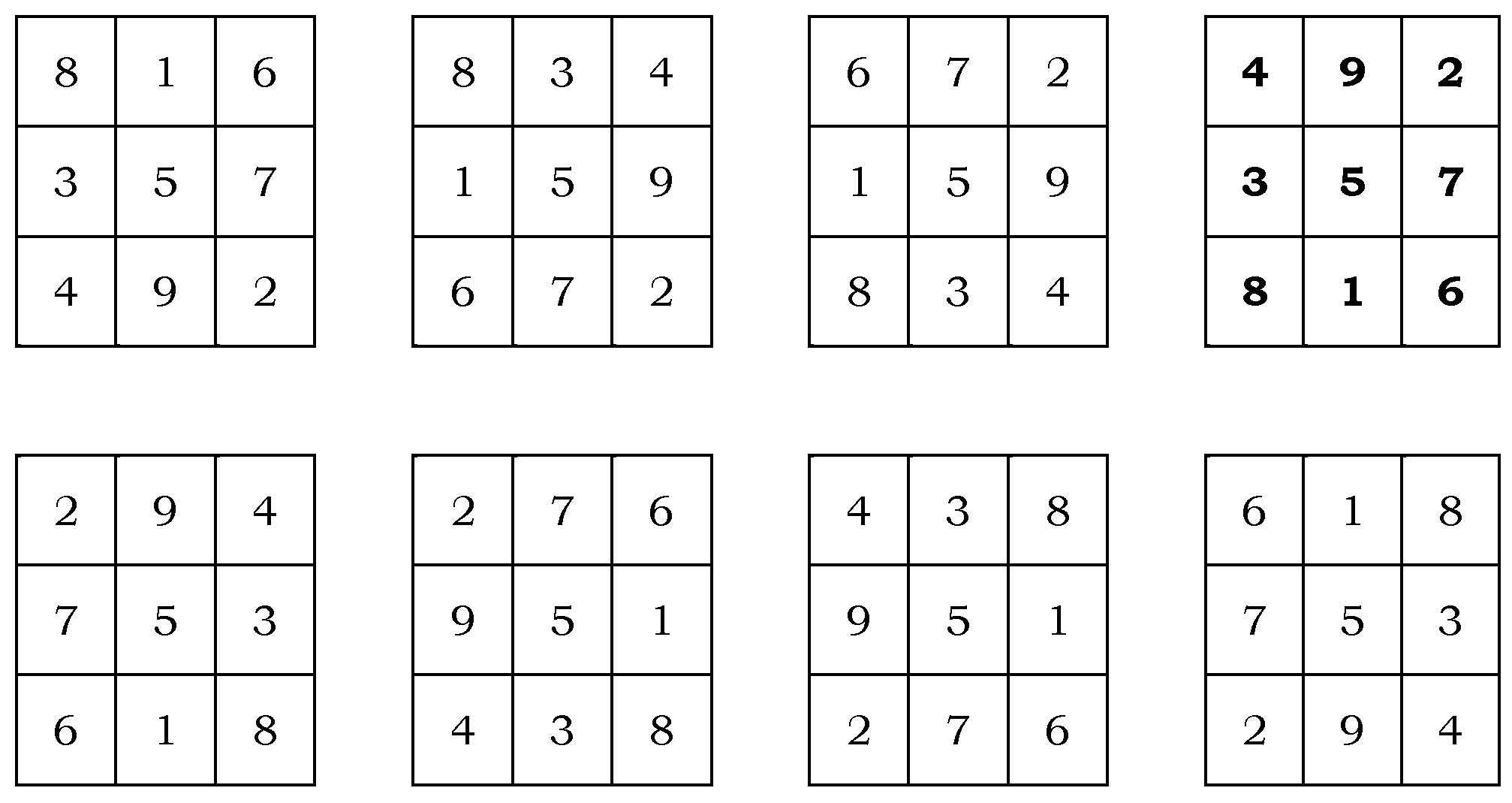"Soluciones" cuadrado mágico 3 x 3

Pero no hagamos trampa: cada uno de los ocho cuadrados mágicos resultantes es realmente el mismo porque se obtiene mediante rotaciones o reflexiones de él; se conviene, pues, que sólo existe una solución auténtica para el cuadrado mágico de 3 x 3, sea cual sea su presentación gráfica.

Sorprendentemente, a partir de 3 x 3, el número de cuadrados mágicos que pueden construirse crece a un ritmo de vértigo. Para el 4 x 4, en el que se encuadra el de Durero, sin considerar rotaciones y reflexiones de la figura, es posible crear 880 cuadrados mágicos diferentes. Para un cuadrado de 5 x 5, el número de resultados posibles (calculado informáticamente en 1973) es de 275.305.224, y para el cuadrado de 6 x 6 ni siquiera se conoce el número, aunque los matemáticos creen como probable la cifra de un 1 seguido de 19 ceros.  

Grabado "Melancolía I", de Durero, donde aparece el cuadrado mágico.

Hay una curiosidad adicional que no nos resistimos a señalar con el cuadrado mágico de Durero, y es que, si se gira 180º y se resta 1 en las casillas que contienen los números 11, 12, 15 y 16 se obtiene el cuadro de Gaudí, que se puede contemplar esculpido en un lateral del Templo de la Sagrada Familia, de Barcelona. Realmente, este cuadrado no es mágico, pues tiene números repetidos, pero es bastante especial: las filas, columnas y diagonales suman 33, la edad de Cristo al morir.  

Cuadrado de Gaudí

Si hablamos de cuadrados mágicos no podemos olvidar a uno de sus estudiosos y entusiasta más notable: Benjamin Franklin, de quien se cuenta que, para matar el aburrimiento que le producían los debates en la Asamblea de Pensilvania, de la que era secretario, construyó una célebre variante de cuadrado de 8 x 8, que publicó en su obra Experiments and observations on electricity, en 1769. Formalmente no es un cuadrado mágico porque, aunque cumple con la regla de las sumas de las filas y de las columnas, siendo la constante del cuadrado 260, no cumple con la regla de la suma de las diagonales principales,sustituídas éstas por "diagonales quebradas", esto es, que partiendo de una esquina, van hacia el centro y vuelven desde él a otra esquina haciendo la forma de una V., y encierra otras simetrías seductoras, como que la suma de los números contenidos en cualquier subcuadrado de 2 x 2 es 130, igual que la suma de cuatro números cualesquiera equidistantes del centro. 

  

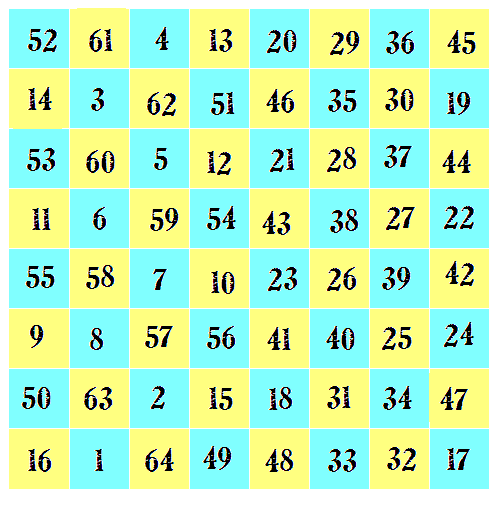Cuadrado 8 x8 Bejamín Franklin

Se dice que Franklin creó varios cuadrados mágicos a lo largo de su vida, y se cuenta como cierta la proeza de que, en una sola tarde, compuso un increíble cuadrado de 16 x 16, que reivindicó como "el más mágicamente mágico de todos los cuadrados mágicos jamás creados por cualquier mago". Sin comentarios.

Cuadrado 16 x 16 Franklin

Y llegamos al sudoku. Ciertamente su base teórica se inspira, aunque sea lejanamente, en los principios matemáticos del cuadrado mágico, pero si bien éste está reservado a mentes auténticamente privilegiadas, el sudoku está pensado para que la gran mayoría de simples mortales puedan acceder ¡y disfrutar! con el pasatiempo. Porque es eso: un pasatiempo.

Contrariamente al cuadrado mágico, cuyo origen se pierde en la noche de los tiempos¹, el sudoku es un invento moderno, de nuestros días, y tiene aquello que llamamos ficha de trazabilidad con fechas, nombres y apellidos. El sudoku, con el nombre de number place, fue inventado en 1979 por el arquitecto americano Howard Garns; fue rediseñado a la forma que le conocemos ahora y bautizado como sudoku (expresión japonesa que se puede traducir por "el número debe aparecer sólo una vez" o, más llano, "solución única") por el japonés Maki Kaji en 1980 y lanzado al gran público a iniciativa del juez jubilado neozelandés Wayne Gould, a través de negociaciones a lo largo del tiempo con empresas editoras de periódicos a partir de 1997. Hay que decir que la aceptación del pasatiempo por el público fue prácticamente inmediata: en 2004 sólo insertaba sudokus en sus páginas el Times; en 2005 se le unió el Daily Telegraph; en 2006 ya publicaban sudokus diarios de sesenta países y, a finales de 2007, ya eran noventa los países, hasta llegar a nuestros días en que se pueden encontrar casi en cualquier diario que caiga en nuestras manos, estemos donde estemos.

Pensando en quien, por diferentes razones, no ha tenido oportunidad de cavilar descifrando los entresijos del juego, diremos que se basa en una tabla (cuadrado latino técnicamente) de 9 x 9 de tal forma que todas las casillas se han de rellenar con dígitos del 1 al 9 con el requisito de que no puede haber ninguna repetición de ningún dígito en ninguna fila ni columna. Hay una condición adicional: el cuadrado de 9 x 9 se divide en 9 subcuadrados de 3 x 3, señalados con un trazo más grueso, y cada número, del 1 al 9, sólo puede aparecer una vez en cada subcuadrado. Para que el juego responda al nombre de sudoku, es decir, tenga una solución única, se proporcionan entre 25 y 30 números/pista correctamente colocados. No es un capricho lo de las pistas correctas: la cadena Sky TV anunció que emitiría un programa sobre sudokus y lanzó como señuelo premiar la correcta resolución de uno de presentación. Con el fin de darle más vidilla al asunto y valorar más la respuesta correcta, de motu propio decidió alterar las pistas (no consta de qué forma, pero cabe pensar que eliminando una). La sorpresa fue que en poco tiempo empezaron a recibir respuestas correctas pero diferentes, lo que representó un fiasco absoluto y el programa no se emitió. Posteriormente se supo que la alteración en lo que devino un falso sudoku daba lugar a obtener 1.950 soluciones correctas.

Hemos apuntado que en los diarios se suelen proponer sudokus con entre 25 y 30 pistas; un ordenador potente, provisto del programa informático adecuado, puede hallar la solución del pasatiempo hasta con un mínimo de 17 pistas, y los expertos matemáticos estiman imposible la resolución de uno con sólo 16 pistas.

La pregunta que es posible que se hagan muchos aficionados es la de si, a la vista de la globalización del pasatiempo, está cercano el tiempo en que se publiquen sudokus repetidos. La respuesta ha de llevarles tranquilidad; aplicando un relativamente sencillo cálculo combinatorio a las premisas de cuadrado latino de 9 x 9 con subcuadrados de 3 x 3 incluyendo cada uno de ellos los dígitos del 1 al 9, el número de cuadrados posibles para ser sudokus es de 6 seguido de 21 ceros. Para no hacer trampas, eliminando los que sean rotaciones o reflexión de otro (como hemos detallado que ocurre en el cuadrado mágico de 3 x 3), el número que queda de posibles sudokus distintos es sólo de unos 6.000 millones. No se acaba el mundo con ellos, no.

¿Alguien se atreve a probar?

------------------------

1El cuadrado mágico de 3 x 3, cuyas filas, columnas y diagonales suman 15, ya aparece citado en la cultura china unos 1200 años antes de nuestra era con el nombre de lo shu, del que creían que simbolizaba las armonías internas del universo, y lo utilizaban para la adivinación y la adoración.